https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/ from Google

Thinking process:

Another hard question from Google. This is a question from Leetcode Weekly Contest 220. One trick for this kind of contest is to always check the constraint first, even before you read the problem statement. By knowing the constraints, your brain will automatically focus on something more feasible, like in the question, you shouldn’t consider any algorithm slower than O(NlogN), so we don’t consider Floyd-Warshall algorithm here.

The most intuitive approach for this is to use dfs for every query, but this is obviously too slow as well. Since it doesn’t work if we do the search for every query, maybe we should start from queries as a whole? like some kind of pre-compute? One thing I can think of is to sort the queries by starting or ending point, so we can group the queries with same starting or ending point together and only do one dfs for each group? However, the worst case will still be E^2 or V^2, so this doesn’t work as well….

After running out of idea, another trick here is to check the tags in Leetcode … There are something like binary search (intersting…but I couldn’t think of how to apply binary search to this…) and union find. Wait, union find!! It seems relate to this proble.

We probably can do union find for each edge? However, union find can only tell us if an edge increases the minimum value for two nodes in different groups like below. It can’t tell us if the query is for two random nodes.

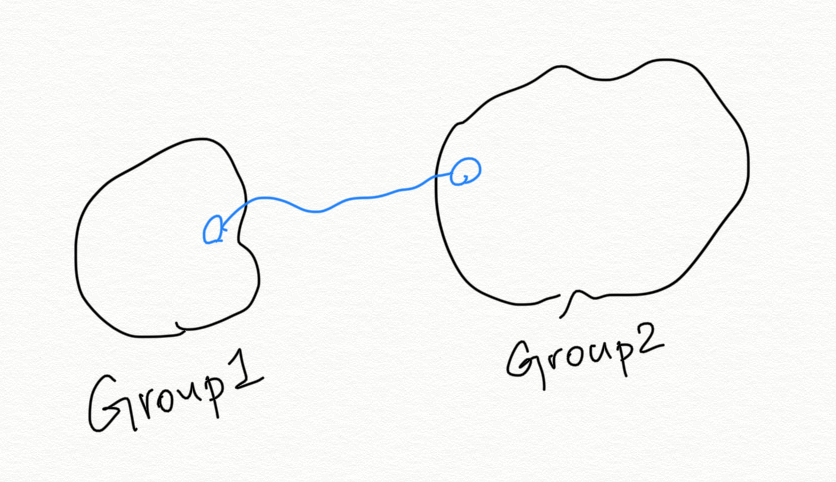
Stuck again :( Again, we probably need to think from queries? So if we know the limit of this query, how can it help? Perhaps we can just union find those edges shorter than the limit? In this way, if two nodes are connected, that means all those edges must be shorter than the limit!

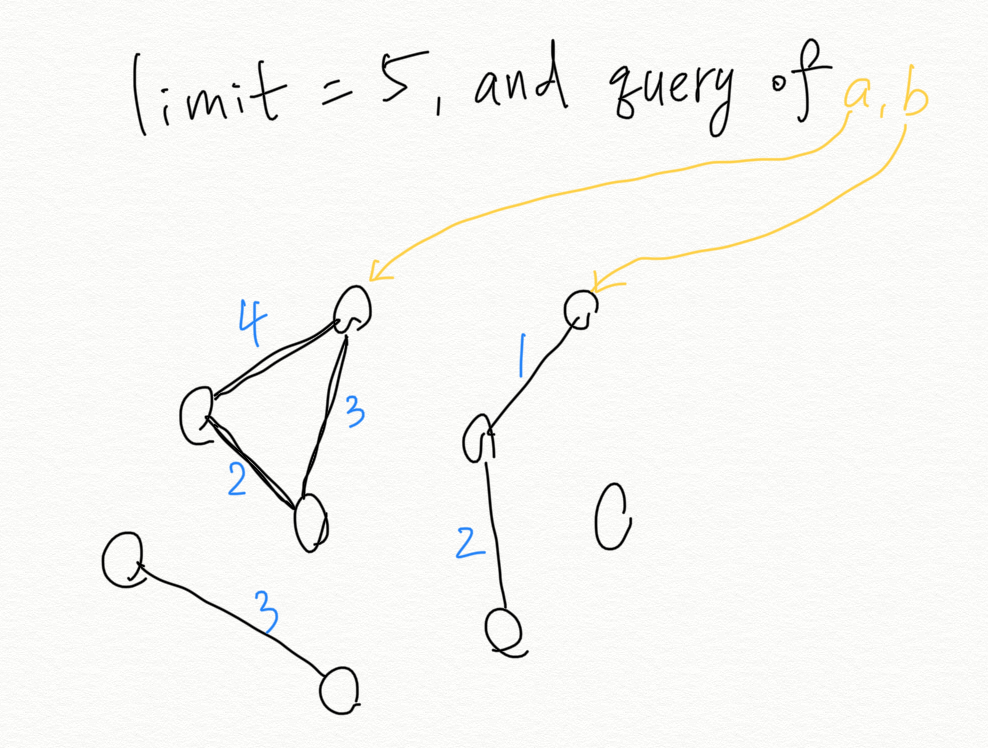
After knowing this, the only thing we need to do is to sort edges and queries, and then for each query, we union those edges shorter than the limit first, and then do a find. If you don’t understand how I implement union find, please find your own template. It’s very important to have a template in interviews.

Here is the code.

 1class Solution {
 2public:
 3    vector<int> p;
 4    int f(int x) {
 5        if (p[x] == x) return x;
 6        return p[x] = f(p[x]);
 7    }
 8    void u(int x, int y) {
 9        int a = f(x);
10        int b = f(y);
11        p[a] = b;
12    }
13    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
14        p.resize(n);
15        for (int i=0; i<n; i++) p[i] = i;
16        int i = 0;
17        int N = edgeList.size();
18        vector<bool> ans(queries.size());
19        
20        sort(edgeList.begin(), edgeList.end(), [](const vector<int>& a, const vector<int>& b) {
21            return a[2] < b[2];
22        });
23        for (auto& q : queries) {
24            q.push_back(i);
25            i++;
26        }
27        sort(queries.begin(), queries.end(), [](const vector<int>& a, const vector<int>& b) {
28            return a[2] < b[2];
29        });
30        
31        i = 0;
32        for (auto q : queries) {
33            int limit = q[2];
34            while (i < N and edgeList[i][2] < limit) {
35                u(edgeList[i][0], edgeList[i][1]);
36                i++;
37            }
38            if (f(q[0]) == f(q[1])) ans[q[3]] = true;
39            else ans[q[3]] = false;
40        }
41        return ans;
42    }
43};