Editorial: LeetCode 1707 Maximum Xor With an Element From Array

https://leetcode.com/problems/maximum-xor-with-an-element-from-array/ from Google
Thinking process:
Look at the constraints here, we know that we need to find the maximum XOR for each query in O(1) or O(logN) time. This is kind of hard as we should do the XOR with every number to know what’s the maximum number. There’s one interesting thing. When you interview with Google, if you have no idea on how to solve the problem, then you might want to consider using Trie. Google ridiculously loves to ask Trie questions. I don’t know why….
Anyways, Trie is basically a compression technique. With that, looks like we can compress all numbers in nums together? Further more, when we go through those numbers, we only need to check 30 times (because they all are less than 30 bits). Just like below
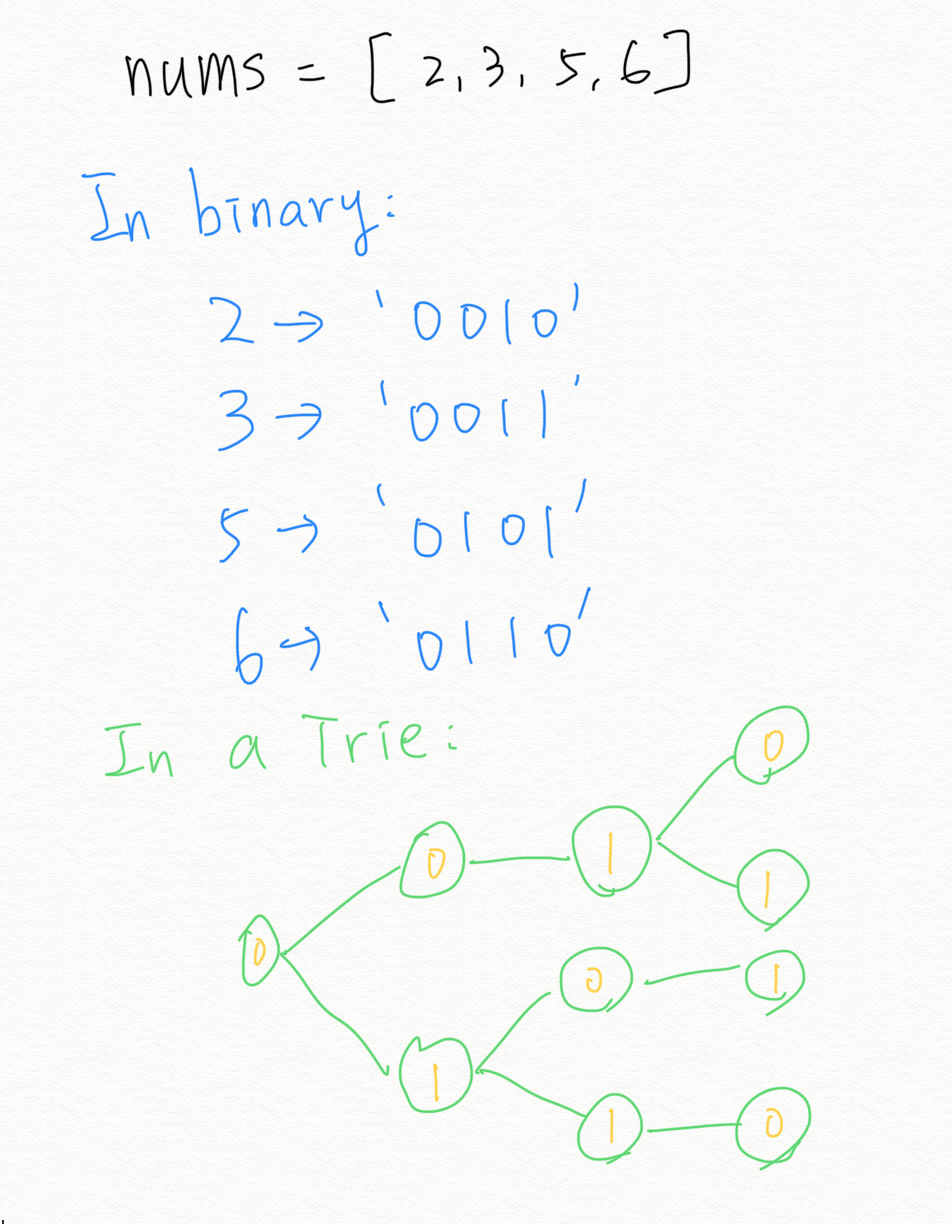
With this Trie, for each query, we only need to go through this Trie based on the x we have. For each bit in x, if it is 1, we want to find a node with value 0 if it’s possible, and vice versa. Finally we just sort our nums and queries to make it easier for us to tell if we need to return a -1.
Here is the code.
1struct Node {
2 struct Node* ch[2];
3};
4class Solution {
5public:
6 void insert(Node* trie, int n) {
7 Node* cur = trie;
8 for (int i=30; i>=0; i--) {
9 int x = (n>>i) & 0x01;
10 if (cur->ch[x] == NULL) {
11 cur->ch[x] = new Node();
12 }
13 cur = cur->ch[x];
14 }
15 }
16 int query(Node* trie, int n) {
17 Node* cur = trie;
18 int ret = 0;
19 for (int i=30; i>=0; i--) {
20 int x = (n>>i) & 0x01;
21 int idx = cur->ch[x^1] == NULL ? x : x^1;
22 if (cur->ch[idx] == NULL) return -1;
23 ret |= ((x^idx) << i);
24 cur = cur->ch[idx];
25 }
26 return ret;
27 }
28 vector<int> maximizeXor(vector<int>& nums, vector<vector<int>>& qs) {
29 int N = nums.size();
30 int Q = qs.size();
31 sort(nums.begin(), nums.end());
32 for (int i=0; i<Q; i++) {
33 qs[i].push_back(i);
34 }
35 sort(qs.begin(), qs.end(), [](const vector<int>& a, const vector<int>& b) {
36 return a[1] < b[1];
37 });
38 int cur = 0;
39 Node* trie = new Node();
40 vector<int> ans(Q);
41 for (auto q : qs) {
42 while (cur < N and nums[cur] <= q[1]) {
43 insert(trie, nums[cur]);
44 cur++;
45 }
46 ans[q[2]] = query(trie, q[0]);
47 }
48 return ans;
49 }
50};