https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii/ from general electric

Thinking process:

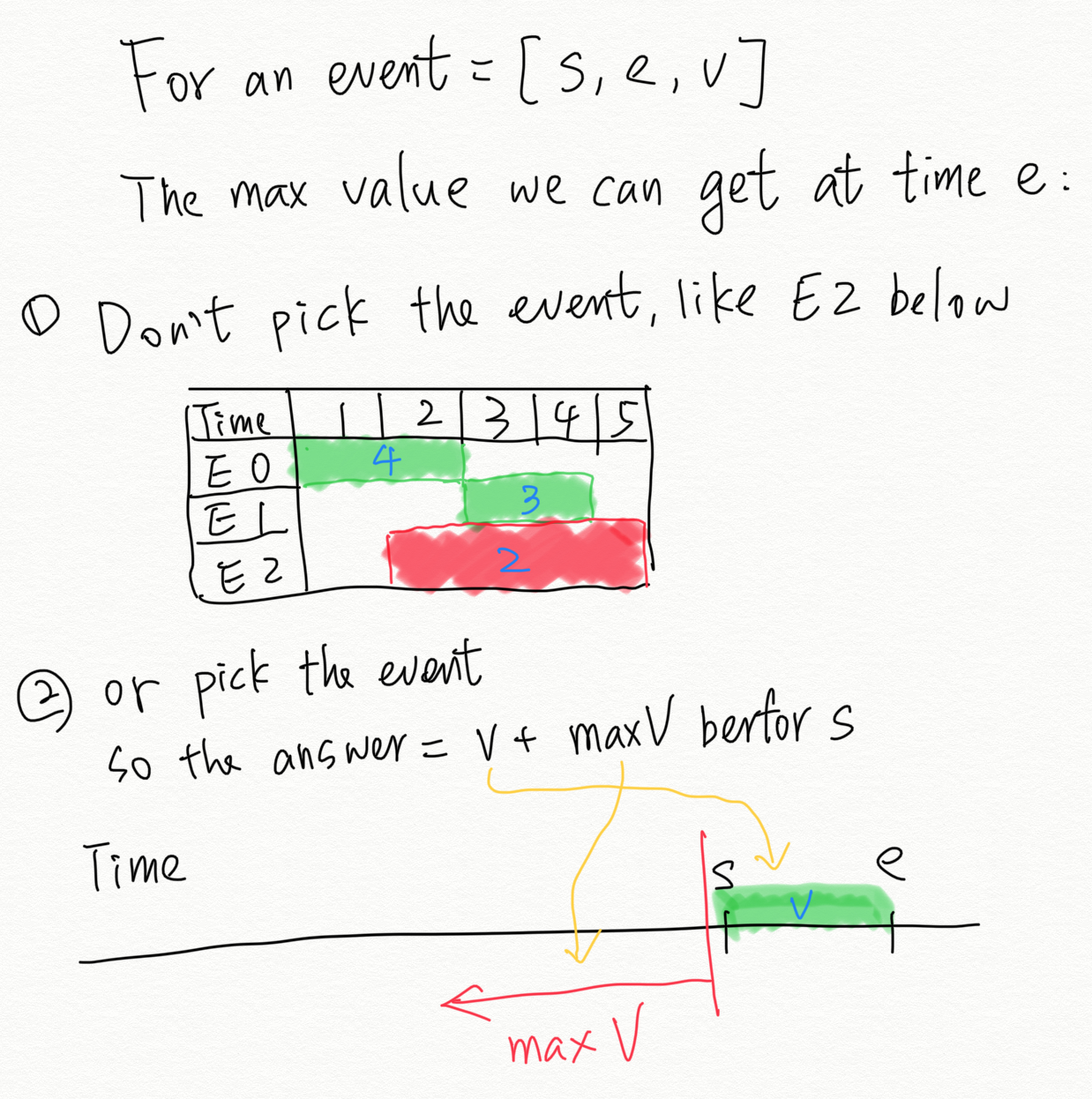
Just think about the brute force way first. Since we can attend at most k events, for any given event ended at time e, the maximum value we can get at time e is: either

• the maximum value we can get if we don’t attend this event
• or the value of this event plus the maximum value we can get before time s (the start time of the event) and the number of events we attend before time s must be less than k.

Then we check the constraint. k * events.length <= 10^6 means we can iterate through events and check if we attend 1 event, 2 events, …, k events already and get the answer and still won’t get a TLE.

This leads us to a dp solution. We can use a map to represent the maximum value we can get (value of the map) at time e (key of the map). We do this k times. In each time, mp means we already attend at most j events, and newMp means we at most attend j+1 events.

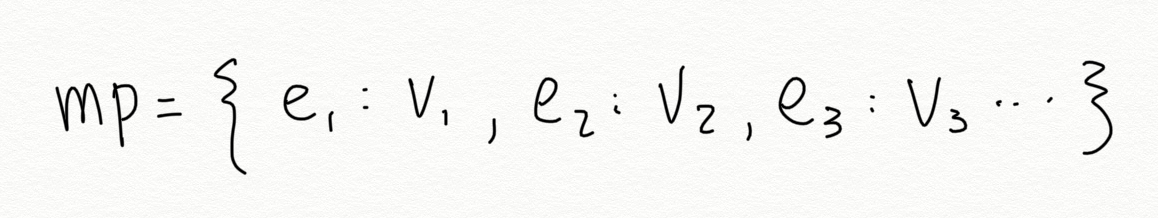
We sort the events according to the end time first to make sure we calculate the earlier event first. Finally, we set newMp[end] to the max of newMp.rbegin()->second and it->second + value. The newMp.rbegin()->second is the “don’t attend this event” case we talk above.

Here is the code.

 1class Solution {
 2public:
 3    int maxValue(vector<vector<int>>& events, int k) {
 4        int N = events.size();
 5        sort(events.begin(), events.end(), [](const auto& e1, const auto& e2) {
 6            return e1[1] < e2[1];
 7        });
 8        map<int, int> mp;
 9        mp[0] = 0;
10        for (int j=0; j<k; j++) {
11            map<int, int> newMp;
12            newMp[0] = 0;
13            for (int i=0; i<N; i++) {
14                auto& e = events[i];
15                int start = e[0], end = e[1], value = e[2];
16                auto it = mp.upper_bound(start-1);
17                it--;
18                newMp[end] = max(newMp.rbegin()->second, it->second + value);
19            }
20            mp = newMp;
21        }
22        return mp.rbegin()->second;
23    }
24};