https://leetcode.com/problems/maximum-subarray-min-product/ from Uber

Thinking process:

The main concept for this question is: for any given element in an array, the min-product must be the longest subarray where all the elements are euqal or bigger than the element we’re given. For example, if the nums = [3,1,6,5,4,5,2], and we want to calculate the min-product of nums[4] (which is 4 in this case), the min-product is 4*(sum of [6, 5, 4, 5]).

And the problem is asking us to find the maximum min-product, which means we just need to iterate through the whole array, and calculate the min-product for each element, then we get the answer. When calculating the min-product, we need the subarray sum, which we can get this by pre computing the prefix sum, which is easy. So, the problem becomes: how to find the boundary efficiently?

One way I can think of is: inserting the element into the array in an increasing order. Let’s use the above array again as the example. As we can see, in this order, we can find the left right boundary easily. We can use an order map where the key is the value of the element, and the value is the index of the element in the array.

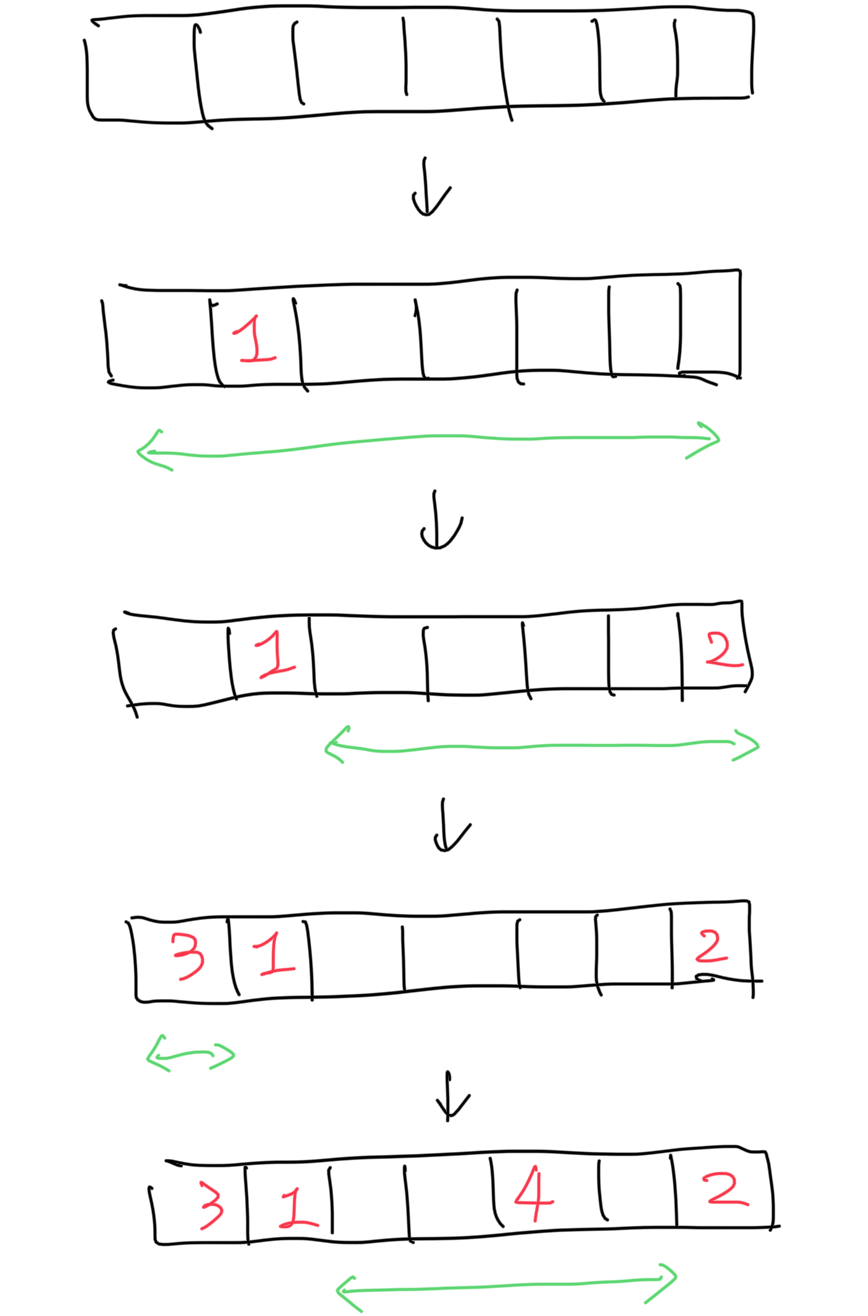
The other way is to use a monostack. We can maintain a non-descreasing stack. If we meet an element which is smaller than any elements in our stack, we pop the element. When we pop the element in our stack, it means we find the left and right boundary. Let’s take the above example again.

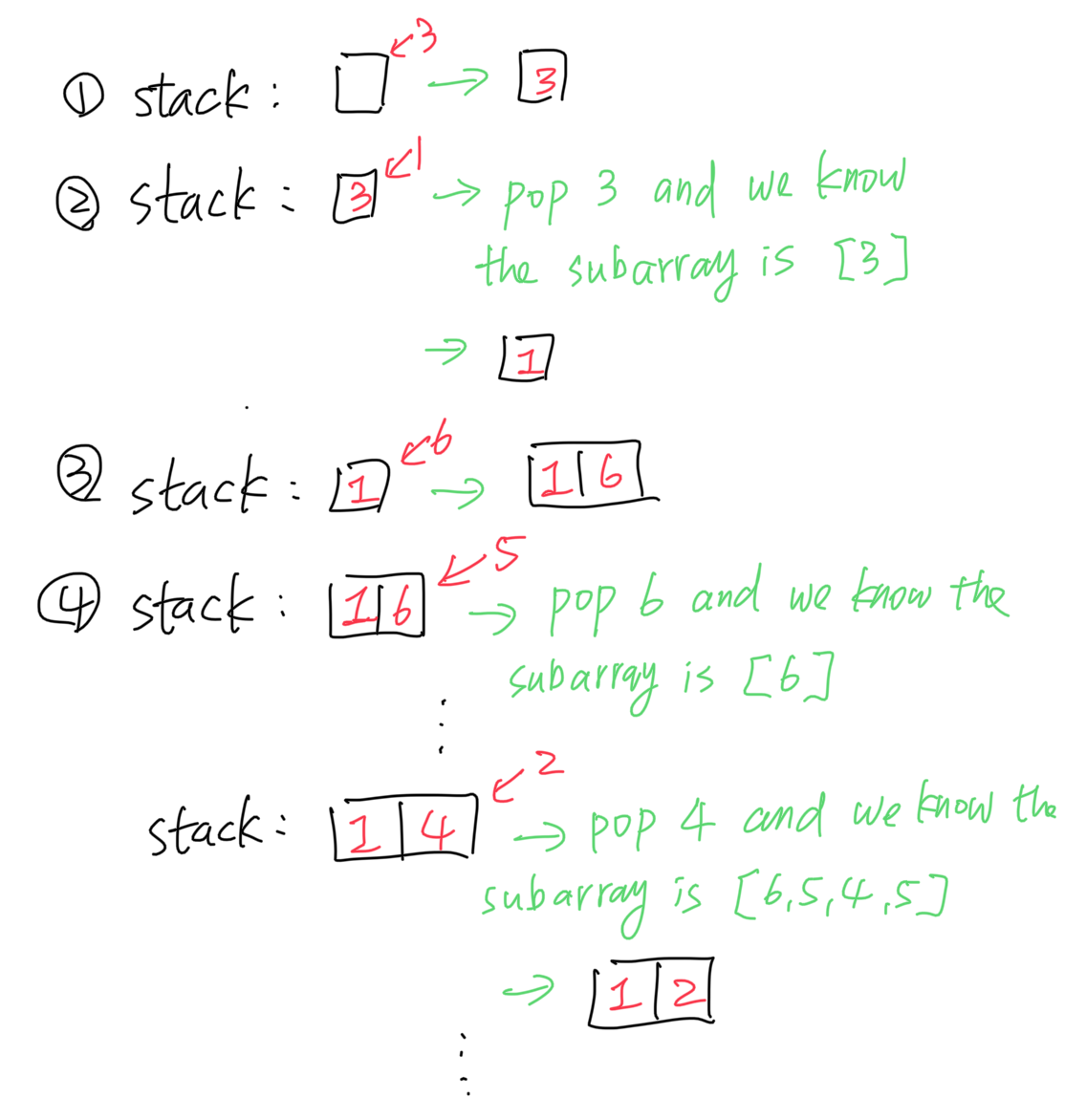
I only implement the code using stack.

Here is the code.

 1class Solution {
 2public:
 3    typedef unsigned long long ll;
 4    int maxSumMinProduct(vector<int>& nums) {
 5        int MOD = 1e9 + 7;
 6        int N = nums.size();
 7        ll sum = 0;
 8        vector<ll> presum(N+1);
 9        for (int i=0; i<N; i++) {
10            sum += nums[i];
11            presum[i+1] = sum;
12        }
13        stack<int> st;
14        ll ans = 0;
15        for (int i=0; i<N; i++) {
16            while (st.size() and nums[st.top()] >= nums[i]) {
17                int j = st.top(); st.pop();
18                int left = st.size() ? st.top() + 1 : 0;
19                ans = max(ans, nums[j]*(presum[i] - presum[left]));
20                // cout << j << " " << left << " " << i << " " << ans << endl;
21            }
22            st.push(i);
23        }
24        while (st.size()) {
25            int j = st.top(); st.pop();
26            int left = st.size() ? st.top() + 1 : 0;
27            ans = max(ans, nums[j]*(presum[N] - presum[left]));
28            // cout << j << " " << left << " " << N-1 << " " << ans << endl;
29        }
30        return ans % MOD;
31    }
32};